I used the wonderful Desmos graphing calculator
to visualize this space:
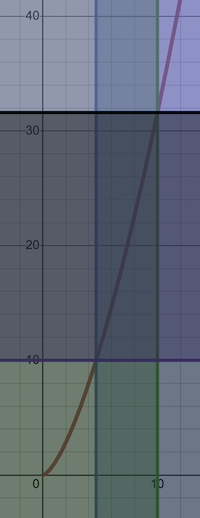
The dark gray rectangle in the middle of the output above is the constrained area of the solution to the problem, and the answer can be gotten by finding the point in that section on the curve that corresponds to integers \(x\) and \(y\). This is somewhat difficult to do with Desmos, but I already knew the answer \((9,27)\), and I did find this point using Desmos' scan functionality.
On the way home from the class, I did some mental figuring, and came to the conclusion that the answer to this puzzle could be gotten by systematically going through the integers 1 through wherever you wanted to stop, and take their 6th power, and these would be the numbers that were cubes as well as squares of some integer. The thinking went something like this: the answer to the puzzle from the book (3-digit number that is a cube and a square) is \(729\), which is \(9\) cubed and \(27\) squared. Well, \(9 = 3^{2}\) and \(27 = 3^{3}\), and \(9^{3} = 27^{2} = 729\), so \((3^{2})^{3} = (3^{3})^{2}\), which is an exponential identity example \(((x^{a})^{b} = (x^{b})^{a} = x^{ab})\). A little mental calculation gave the 2-digit cube/square number as \(64 = 2^{6}\), which backed up the hypothesis. So, to get the numbers which are both cubes and sqaures (of integers, by definition), all I needed to do was to write a Pascal program that listed the numbers which were 6th powers of each of the integers from 1 to whatever number I wanted to go up to.
When I got home, I started writing the program, and with a lot of looking up for syntax, and adding the counting of digits to make it a more interesting problem discussion for the class, I came up with a program which produced the desired output.
But after thinking about it for a while, I decided that Javascript would be a better solution, since this language was made for HTML and browsers, and I've done a fair amount of programming in it for another venture. Here's the result:
The digit-count is in parentheses, as you might have surmised. So, as the problem statement above says, there is only one 3-digit number that is both a cube and a square. It turns out there is another problem in the puzzle book just before the one I gave asking for the 2-digit number that is a cube and a square, and we can see, as the book notes, that the answer is \(64\). There is also only one 4-digit solution \((4096 = 4^{6} = 2^{12})\), two 5-digit solutions, three 6-digit solutions, five 7-digit solutions, and so on. I'm trying to see whether there is any pattern to the number of digit solutions, but haven't discovered anything obvious yet. One pretty cool pattern to note is that the ones digit (farthest to the right) of the solutions go in the repeating pattern \(1, 4, 9, 6, 5, 6, 9, 4, 1, 0\). If you include \(0\) in the integer list, this becomes a palindrome: \(01496569410\). Cool!
And this is only one of the hundreds of puzzles included in this short book of puzzles! Imagine how much fun we'll have solving some of the others!!

The dark gray rectangle in the middle of the output above is the constrained area of the solution to the problem, and the answer can be gotten by finding the point in that section on the curve that corresponds to integers \(x\) and \(y\). This is somewhat difficult to do with Desmos, but I already knew the answer \((9,27)\), and I did find this point using Desmos' scan functionality.
On the way home from the class, I did some mental figuring, and came to the conclusion that the answer to this puzzle could be gotten by systematically going through the integers 1 through wherever you wanted to stop, and take their 6th power, and these would be the numbers that were cubes as well as squares of some integer. The thinking went something like this: the answer to the puzzle from the book (3-digit number that is a cube and a square) is \(729\), which is \(9\) cubed and \(27\) squared. Well, \(9 = 3^{2}\) and \(27 = 3^{3}\), and \(9^{3} = 27^{2} = 729\), so \((3^{2})^{3} = (3^{3})^{2}\), which is an exponential identity example \(((x^{a})^{b} = (x^{b})^{a} = x^{ab})\). A little mental calculation gave the 2-digit cube/square number as \(64 = 2^{6}\), which backed up the hypothesis. So, to get the numbers which are both cubes and sqaures (of integers, by definition), all I needed to do was to write a Pascal program that listed the numbers which were 6th powers of each of the integers from 1 to whatever number I wanted to go up to.
When I got home, I started writing the program, and with a lot of looking up for syntax, and adding the counting of digits to make it a more interesting problem discussion for the class, I came up with a program which produced the desired output.
But after thinking about it for a while, I decided that Javascript would be a better solution, since this language was made for HTML and browsers, and I've done a fair amount of programming in it for another venture. Here's the result:
The digit-count is in parentheses, as you might have surmised. So, as the problem statement above says, there is only one 3-digit number that is both a cube and a square. It turns out there is another problem in the puzzle book just before the one I gave asking for the 2-digit number that is a cube and a square, and we can see, as the book notes, that the answer is \(64\). There is also only one 4-digit solution \((4096 = 4^{6} = 2^{12})\), two 5-digit solutions, three 6-digit solutions, five 7-digit solutions, and so on. I'm trying to see whether there is any pattern to the number of digit solutions, but haven't discovered anything obvious yet. One pretty cool pattern to note is that the ones digit (farthest to the right) of the solutions go in the repeating pattern \(1, 4, 9, 6, 5, 6, 9, 4, 1, 0\). If you include \(0\) in the integer list, this becomes a palindrome: \(01496569410\). Cool!
And this is only one of the hundreds of puzzles included in this short book of puzzles! Imagine how much fun we'll have solving some of the others!!