
Recently, I asked the North Coast Puzzle Club to work on a problem that came from a substitute teacher job I had the previous week. In the math sectionfor a 4th/5th grade class, the teacher said to "teach area and perimeter," so I drew a pentagon on the electronic board and asked the class to determine its area. The formula for the area of a regular pentagon is a bit complicated, and after several students answered the question with some variation on "length times width" I coaxed out of them the idea of drawing a regular pentagon on a piece of graph paper and estimating its area by counting the squares inside the shape.
For the puzzle club exercise, I asked members to draw different regular polygons on graph paper and count squares. The idea was to maybe determine a pattern in the areas, or figure out a formula of some kind. Well, the exercise bogged down in practical terms, as it is quite difficult to draw regular polygons with only a ruler, pencil and graph paper. I took the papers of the group home to see if I could determine some pattern in what they did, but I was unable to find one. So I eventually succumbed to the use of the internet to find areas of the first few regular polygons (triangle up to decagon) with side lengths of \(10\). There may be a general formula for the area of any regular polygon, but I haven't really looked yet.
I took the areas, \(A\), of the regular polygons of side length \(10\), together with the amount of sides, \(n\), and made a table in Desmos, and graphed the result. Here's the table, using a regular polygon area calculator on the web and rounding the areas to the nearest integer:
\[ \begin{matrix} sides & area \\ 3 & 43 \\ 4 & 100 \\ 5 & 172 \\ 6 & 260 \\ 7 & 363 \\ 8 & 483 \\ 9 & 618 \\ 10 & 769 \end{matrix} \]
Then I tried various functions to fit the points on a curve. After a little manipulation, I got this function:
\[y=8x^2-28\]
as the closest fit to all the points, with:
\[y=8x^2-x-25\]
as second best.
Pretty good, but would this work for any side length, \(s\)? Well, of course I tried \(s=1\) and the graph and function was just scaled by \(100\), or \(10^2\), so I divided the coefficients in the first equation by \(100\) and got:
\[y=0.08x^2-0.28\]
for side length \(1\), which worked fine.
So, now I guessed at what would be needed to adjust for any side length, and after substituting in different variable names (\(s\) for side length, \(n\) for number of sides, and \(A\) for area) and factoring, I got:
\[\boxed{A=0.04s^2(2n^2-7)=\frac{(2n^2-7)s^2}{25}}\]
which works surprisingly well for regular polygons up to \(n=10\). Here's the table for side length \(s=10\) with the area calculator result and the above formula result for \(n=3-10\):
\[ \begin{matrix} sides & area(web) & area(formula) \\ 3 & 43 & 44 \\ 4 & 100 & 100 \\ 5 & 172 & 172 \\ 6 & 260 & 260 \\ 7 & 363 & 364 \\ 8 & 483 & 484 \\ 9 & 618 & 620 \\ 10 & 769 & 772 \end{matrix} \]
Another way to look at this formula is to look at the \(\frac{2n^2-7}{25}\) part as a coefficient to the \(s^2\), or as a scaling factor. So, area of a regular polygon could be seen as a function of the length of a side squared, which kind of makes sense, since these are two-dimensional figures with equal sides. Here are the scaling factors for \(n=3-10\):
\[ \begin{matrix} sides & scaling factor \\ 3 & 0.44 \\ 4 & 1 \\ 5 & 1.72 \\ 6 & 2.6 \\ 7 & 3.64 \\ 8 & 4.84 \\ 9 & 6.2 \\ 10 & 7.72 \end{matrix} \]
The quadratic polynomial I used had a little trouble with \(n=3\) and was starting to be more than \(1\) different from the web calculator at \(n=9\), at least for \(s=10\). For such a simple formula, however, it works amazingly well over a fairly large range of regular polygons. Additional work will be necessary to refine the model and see for what side length (\(s\)) ranges it works well.
Looking up the formula for the area of a polygon of \(n\) sides, with each side \(s\) units long, it is:
\[A=\frac{s^{2}n}{4\tan\left(\frac{180°}{n}\right)}\]
Using this formula to calculate the areas of regular polygons from a triangle to a decagon, and comparing it to my formula above, with a side length \(s\) of \(10\) units gives the same results as above, so either they used this formula on the other website, or something equivalent. The formula for area of regular polygons comes from an analysis of the problem by splitting the polygon into triangles and adding up the areas of those triangles. That's where the trigonometric function comes in. The advantage of my formula is that at least for these small values of \(s\) and \(n\), there are no trigonometric calculations necessary. While my formula is just an estimate, the error in area is small up to a decagon. Perhaps more important, it appears to be a novel way of calculating area of regular polygons, all coming from the educational angle of exploring area by counting unit squares and fitting a curve to a set of points. Cool!
As mentioned above, it proved pretty much impossible to draw regular polygons on a grid with only a ruler (can it be proved that you can't?). So I looked up drawing regular polygons on a grid using computer applications, and the first search result was from Mathigon, which I've used in the past and is a fantastic app for learning math. The Polypad function, which allows students and anyone else to explore using all kinds of mathematical objects, has moved to the Amplify platform, and I produced the screenshot below of the first 6 regular polygons for this page using Amplify Polypad. Each polygon has a side length of 4 grid units.

Counting the squares for each polygon to determine the area is only trivial in the case of the square, which obviously has 16 squares in it. The triangle appear to have a little less than half the squares, but counting them involves a fair amount of estimation. To get a little better handle on area via counting squares, we can use the awesome sankaku puzzles by the Japanese educator Naoki Inaba, who has produced an amazing amount of puzzles for math students and the general public. In these puzzles, the user is asked to connect dots on a grid to form triangles of a designated area. Here is an example and a quick explanation of how to solve these puzzles from Inaba's website (in Japanese):
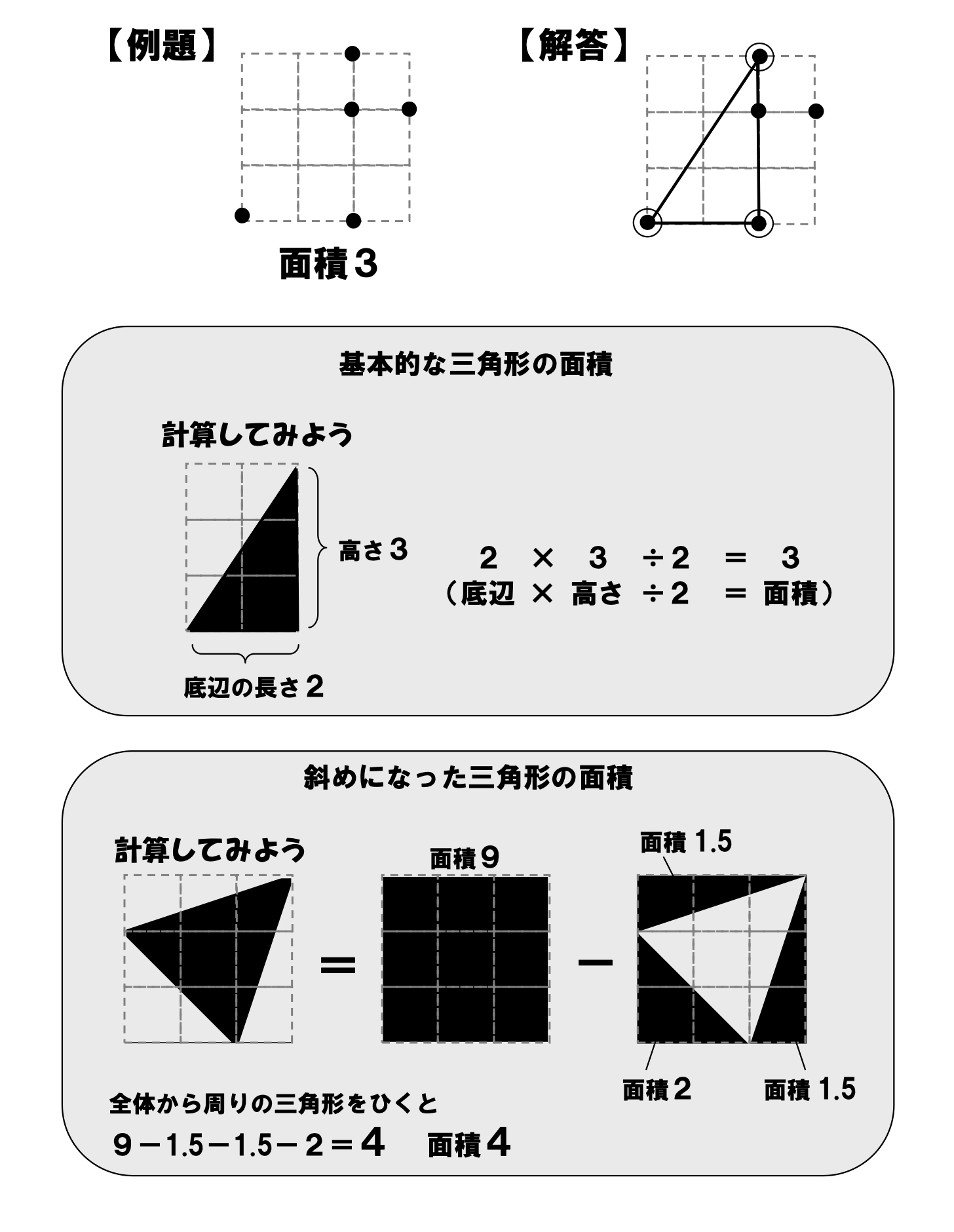
This is relatively easy to solve with vertices of triangles on the grid intersections, but you can see that most of the vertices of the regular polygons above are not at grid intersections (except the ones I put there in Polypad). So we'll have to employ some geometry and maybe even estimation to the problem. I'm currently working on this, and will update this page when I make more progress.