Chemistry Crossword #1 | Cube and Square | Balancing Chemical Equations Using Systems of Algebraic Equations | Some Alphametic Puzzles | Play insumnia | My First Crossnumber Puzzle! | Puzzle Resources for Upward Bound Math Class | The Full Crossnumber Puzzle! | Chemish | By The Numbers Crossword | CCC Community Education Puzzles Class | Astoria Teachers Puzzles Class | North Coast Puzzle Club
Here you will find all sorts of resources and examples of puzzles of all types. Deriving from Bob's experience in teaching math to Upward Bound students the past two summers and his love of number puzzles and games, two courses have already been completed, which you can find the notes for above in the menu – just go to the CCC Community Education Puzzles Class and Astoria Teachers Puzzles Class links above.
The North Coast Puzzle Club (NCPC or NikPik (it's no picnic, or is it?)) has been meeting for a few months, and gaining members little by little. This idea came out of the community education class, and we already have a few excited members ready to meet and create, find and solve puzzles of all types! Just go to the North Coast Puzzle Club link above, or hit the button.
As time goes on, this page may change a bit, but for now, click through the links above to get an idea of the kinds of puzzles we have been creating and solving to date, and to try some yourself. Enjoy!
1. I Spy... – This is a game you can play with a deck of regular playing cards or Uno cards. Take away all the picture cards (or not) or the Uno special cards, and lay out the cards in a grid (as close to square as you can get). Then have one player say, "I spy a sum of x", where x = the sum of two adjacent cards, either up and down or across (no diagonals). This is a game Bob learned at Astor Elementary School recently. For the grades there (K-2), the rules are usually sums, and usually of only two adjacent cards, but you can change the rules to include more than two adjacent cards, non-adjacent cards, differences, products and quotients, or any other arithmetical operation or procedure. The idea is that the opposing player or players get to try to find the cards you spied, and they collect the cards from all instances of that sum, difference, etc. until they give up. If the particular instance that you spied doesn't get discovered, then you get those cards. The player with the most cards wins. It's a variation of Krypto and other target-based games, and all you need is a deck of cards. Uno cards work quite well with this game, and they are typically present in most classrooms.
2. Check this out – Balance Quest Puzzles! Here's the explanation from the website: "Balance Quest puzzles are mathemetical logic problems. Each puzzle contains a large grid comprised of grey and white cells - some are pre-filled with numbers, others are empty. Your task is to fill every empty cell with a positive or negative integer in such a way so that each white cell's value equals the sum of its adjoining half-height cells. When complete, each Balance Quest puzzle grid will "balance" itself in such a way so that the four center cells surrouding the center "zero cell" will always add up to zero. Each puzzle has one, and only one, unique solution."
3. Add this site to your daily puzzle adventures: Sumplete. It's a math logic puzzle with lots of levels of difficulty that asks you to keep and delete numbers in a square grid that add up to the given number in the margin. Inspired by Suduko, Kakuro and Hitori, and developed with ChatGPT!
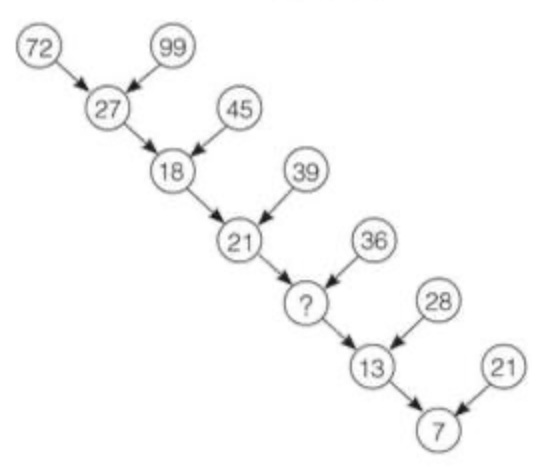
4. The Japanese puzzle inventor Nob Yoshigahara considered this puzzle his masterpiece. The numbers below are arranged according to a certain rule. Once you've worked out the rule, fill in the missing number. The number 7 in the final circle is not a typographical error. See here for the solution. By the way, the Brain Easer website, where the solution to Nob's number tree problem comes from in the previous sentence, is a great website for puzzlers! We should take a look at this site at puzzle club! And while looking for other similar puzzles, Bob came across the T Puzzle, which is a tiling puzzle that supposedly is actually quite hard, though when you see the solution, you'll wonder why it took you so long! And check out Hanayama Toys, a company Yoshigahara made many puzzles for. Mostly mechanical puzzles which NikPikkers might really enjoy!

5. The Puzzle Society is a website with lots of games and puzzles. I'm a fan of the old newspaper Jumble puzzles, and there's one on this site that isn't bad. Give it a look!
6. Bob has found a game that goes by the name The Uzzle (get it?), and maybe will buy it to see if NikPik members like it. It's a pattern matching game, where you have cubes with patterns on them, and you have to reproduce the patterns on a card. They claim to have enough cards and cubes for 10 years of playing without a repeat!
7. On a lovely site called Math Equals Love, there's a page of logic puzzles by the puzzle meister Naomi Inaba. Take a look and try your hand at these. Most are reasonably easy, but kind of fun. Bob is fond of a few of these Inaba puzzle types, including zukei, shikaku and mizu. Zukei is shape recognition, shikaku is grid cutting into rectangles, and mizu is a Yohaku-type puzzle with fractions using water (volume) filling as a metaphor. To start, pick a type of puzzle you think you'd enjoy, and give some of that type a try. Be thinking about how to create some of these puzzles...
8. In looking up Back Spin, Bob came across another solitaire game from Think Fun called solitaire chess. Wanting to introduce this to NikPik, he found a couple on-line versions of the game. The first is called Solitaire Chess from SilverGames.com, and has a small board like the physical version from Think Fun. It's one of those flashing lights sites with lots of ads, but the game itself is pretty good. The second one he found has a full board, is called Solo Chess, and is one of the puzzles from the chess site chess.com. Great site with lots of free puzzles and training for becoming great at chess! If you are at all interested in chess, or in other strategic, constrained movement puzzles or games, these puzzles will be interesting. The skill levels have a humungous range, so you can play or train at whatever level you want.
9. Let's try some tangrams! Take a look at this page, Mathigon Tangrams. I had the 2nd graders doing these, and they did a lot better than me! If anyone has any physical tangram sets, please bring them to NikPik. Here's some background from the Byju's website: The tangrams are old Chinese puzzles. From the pieces of the tangram, we can make many shapes of animals, people and things. The tangram is an operation puzzle consisting of seven flat polygons, called tans, which are put together to form shapes. The main objective of making tangrams is to replicate a shape by giving only an outline in a puzzle book with the help of all seven pieces without overlap. Alternatively, to generate unique minimalist patterns or designs that are either recognized for their inherent artistic values or as the foundation for challenging others to replicate its outline, we can use the tans. Industrialist Friedrich Adolf Richter first introduced tangrams around the 18th century to the German public. The sets were made out of stone or false earthenware and marketed under “The Anchor Puzzle”. More globally, World War I saw a remarkable resurgence of attention in tangrams on the homefront and trenches of both sides. It was performed under the name of “The Sphinx”, an alternative name for the “Anchor Puzzle” sets.
The classic rules that are applied to make tangrams include:
By following the above conditions, we can form various tangram pictures such as:
For some examples of objects you can make from the standard tans, see the ByJu's tangram page. More general information on tangrams here.